Descriptive Analysis

Image by : NASA

Data Analysis Questions: Descriptive Statistics
Tell me the summary of what happened

‘The saddest summary of a life contains 3 descriptions : could have, might have, should have’

Every data analysis process begins with a critical question and we expect the answer of it, is going to give insight of how to solve a problem.
This is the most important step in a data analysis pipeline, asking the right question and find the dataset that will support this question.

‘I checked it very thoroughly’,said the computer, ‘and that quite definitely is the answer.’
‘I think the problem, to be honest, is that I may never actually known what the question is’, said the scientist.

What we can learn from data can be categorized at five types of analysis questions:

1. Descriptive
2. Exploratory
3. Referential
4. Predictive
5. Causal

What have in common the below questions?

• What are the most important factors that influence the career choices of Japanese students?
• Did users like the new cd of Ben Howard based on the number of tweets?
• How often do Greek university students use Facebook each week?
• What percent of the population voted against Brexit?
• How many users visited my site?

Yes, we reinvent the wheel, they are all descriptive. So what is the purpose of a descriptive question?
Descriptive statistics use numbers to summarize the essence of a data set, they answer ‘what happened’ via frequencies, central tendency or measure of spread. We approach them from the perspective of explaining the most common functions used by data analysis tools like Octave, MatLab, Excel, R.

In this post, you’ll read about:

1. Descriptive Analysis
2. Central Tendency: Mean, Median, Mode.
3. Measure of Spread: Range, Interquartile range, Variance, Standard Deviation, Skewness, Kurtosis
4. Measure of Frequency Distributions: Histograms for quantitative data ponts
5. Why do we care about data distribution?

Let’s see an example more closely:
Let’s say that each value of the dataset represents the number of users that visit your website during the first five days that you lunch it.

1
2
3
4
5
6
7
8
9
10

The dataset:
a = 150 users on Monday,
b = 100 users on Tuesday,
c = 21 users on Wednesday,
d = 21 users on Thursday, 
e = 50 users on Friday
N = 5 which is the population, because we are using the entire set of possible values. 
Sample n = 4 or 3 or 2 or 1, if we were not using the entire set of possible values.

Though, this example does not correspond to real-life problems since the number of data points is too small and there is no randomness in data selection. Hence, data are not representative of the population, which introduces the bias. In our example, a selection bias would be that on Monday & Tuesday, we have got many visitors since these days succeed weekend, in which users have not access to our site. The story is trully science fiction; I mean, what kind of site is not running on weekends?

1. Central Tedency
Mean: ‘How representative is the data set?’
We do not use the mean when there are many outliers or many missing values

1
2

Mean: 68.4
Average of all values: a + b + c + d + e / N

Median: the value(s) of which both right and left, lie the 50% of the remaining data points;
put all the values in a descending order, and:

if the number of data points is odd: median = median_i
else median = 1/2 (median _i + median _i+1)

1
2
3

Median: 50
The middle value in a sequence of values that are put in order regarding to their size
21, 21, 50, 100, 150.

The mode usually used either accompanied with the two aforementioned measures or for the computation of categorical values’ central tedency. It is the data point with the higher frequency

1
2

Mode: 21
The value that occurs most frequently within a set of values.

2. Measures of Variability
Knowing the cental tedency of data points is not adequate for estimating the representativeness of the dataset,; since different data shapes can have the same mean, median or mode. It is useful to know the the size of a dispersion, as well.

The range is changed every time a new data point is added. It is not much reliable, since it’s affected only by the outliers.

1
2

Range: 129 
Maximum - Minimum Value

1

Maximum & Minimum Value: 150, 21

The interquartile range covers the 50% of data points distributio, and is defined as the difference of quartiles: Q3 - Q2. It is used usually together with the mode. Though, the most reliable measures of variability are variance and standard deviation because the use as benchbark the mean and they take into accout all the distances of data points from it.

Variance shows us the average dispersion from the center. The expected value of sample variance converges to sample population and this means that variance is a very good measure.
There are many ways to calculate the variance and the most popular is the one that includes the computation of the mean.

1
2
3
4

Variance: = 2.497,84
The average of the squared differences from the mean: 81.6^2 +31.6^ 2 + (-47.4)^ 2+ -(47.4)^2 + (-18.4)^2/5
Since: The difference of *a* from the mean: 150 – 68.4 = 81.6, of *b* is 100 – 68.4 = 31.6 and so forth.
If we have a sample instead of population, our denominator would be n-1.

The standard deviation measures how spread out the variables are. Just to note that, the standard deviation of the sample is not an unbiased estimate for population since its expected value does not converge to population standard deviation. Since the concept of expected values falls out of our current scope, this is not important to remember right now.

1
2

Standard Deviation: 49.9783
The squared root of variance.

3. Data Set Shape & Frequency Distributions
Equally useful is to know the shape of the data set, namely if the data points are massed to the left or right of the mean?

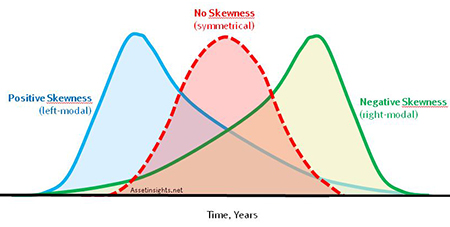
Skewness describes the long-tail of the distribution and it can be negative, positive, without skewness or undefined. Consider for instance the income distribution as long right tail(the blue one). This shows the inequality in income since the average of income is above the median and mode.

1
2
3

Skewness: 0.56981, Moderately skewed
It measures the lack of symmetry of the data set’s probability distribution.
 ((a-mean)^3 +  (b-mean)^3 +  (c-mean)^3 +  (d-mean)^3 + (e-mean)^3)) / standard deviation^3 * n

1
2

Kurtosis:  1.7805
 ((a-mean)^4 +  (b-mean)^4 +  (c-mean)^4 +  (d-mean)^4 + (e-mean)^4)) / standard deviation^4 * n

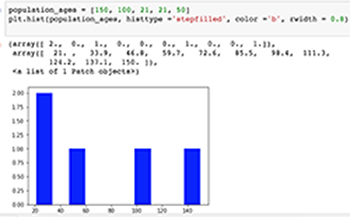
Why do we care about distribution?
Probability distributions are listing every probability such as ‘how likely is the route to my work to be 10-20 minutes’, ‘how likely to be 30-40 minute route’ and so forth’.

Many social and nature phenomena are probabilistic; and engineers, scientists and policy makers often use probability to model and predict system behavior. -Sanjoy Mahajan

Many data analysis functions have as a prerequisite for data to follow a normal distribution or other. Otherwise, we take an inaccurate answer since the math behind it are based on an assumption of a normal distribution or other.
To put it differently, from the view of an engineer. When designing a learning algorithm, should firstly be defined what is the real-world problem that must be soved with the algorithm. Before modelling this problem to math prepositions, we must define the objects of interest in a structured form. The distribution shows us the different values these objects could take(range), what it is considered as the ‘normal’(mean) and what as ‘rare’(outliers). If these assumptions regarding probability distribution, namely data representativenessⁱ, is false, then the algorithm will produce inaccurate outputs.
Sometimes,

There are also some other functions like percentile, moment, correlation coefficients, covariance, and confidence level percentage but in the favour of simplicity, let’s discuss them in another post.
When you are using statistical tools, you don’t need to know exactly what the funtion is since you just heve to call the name of the function and you get the result, as I computed the results for the example using Octave ¹. But to understand the results we have to be serious and know at least the basic idea behind the function we are calling. The sampe applies to machine learning models using the sklearn library